Dispersion of White light analysis, Normal prism and thin prism

When a light ray falls on a triangular prism in a certain position, it emerges from the prism, dispersed into a rainbow, There are two types of triangular prism which are normal prism and thin prism, But rectangular glass does not disperse the light because it acts as two similar reversed prisms, one cancel the dispersion of the other.

Normal prism

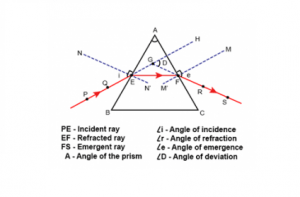
If a light ray falls on the face of the prism, it refracts inside the prism until it falls on the second face and emerges from the prism, The light ray refracts twice, The light ray deviates from its path by a certain angle, which is called angle of deviation (α).

Angle of deviation (α) is the angle subtended by the direction of the extension of the incident ray and the emerging ray in a triangular prism, Apex angle (A) is the confined angle between the two sides of the prism, one of them, the light ray falls on it and the other, the light ray emerges from it.

When the angle of deviation of a triangular prism = 35°, this means that the angle is subtended by the directions of the extension of the incident ray and the emerging ray = 35°.

Deduction of the laws of a triangular prism

The apex angle of the prism (A): A = Θ₁ + Φ₂

Where: Θ₁ is the angle of refraction at the first surface and Φ₂ is the angle of incidence at the second surface.

The angle of deviation (α) :  α = (Φ₁ − Θ₁) + (Θ₂ − Φ₂)

Where: Φ₁ is the angle of incidence at the first surface and Θ₂ is the angle of emergence.

α = (Φ₁ + Θ₂) − A

Tracing the path of the light ray in the triangular prism:

First: The angle of incidence on the first surface (Φ₁) 

When  Φ₁ > 0°, The light ray refracts inside the prism and falls on the other surface.

sin Θ₁ = sin Φ₁ / n , A = Θ₁ + Φ₂

When  Φ₁ = 0°, The light ray passes without any refraction.

Φ₁ = Θ₁ = 0° , A = Φ₂

Second: The angle of incidence on the second surface (Φ₂):

When Φ₂ > Φ_c (the critical angle of the prism), The light ray reflects totally inside the prism.

The angle of incidence = Angle of reflection.

When  Φ₂ <  Φ_c, The light ray refracts and emerges from the prism near the separating surface (away from the normal).

sin Θ₂ = n sin Φ₂ 

Third: The angle of emergence (Θ₂).

When Θ₂ = 90°, The light ray emerges tangent to the separating surface.

Φ₂ = Φ_c  , A = Θ₁ + Φ_c

When Θ₂ = 0°, The light ray emerges normal to the opposite surface of the prism.

Φ₂ = Θ₂ = 0° , A = Θ₁

Factors affect the angle of deviation in the triangular prism 

According to the relation: α = (Φ₁ + Θ₂) − A

The angle of deviation in a prism of apex (A) depends on the angle of incidence (Φ₁) only, The angle of deviation decreases as the angle of incidence (Φ₁) increases until it reaches its minimum value (α_o) and then increases again by increasing (Φ₁), The value of (α_o) is called the minimum angle of deviation.

Conditions of the minimum angle of deviation:

1. The angle of incidence (Φ₁) equals the angle of emergence (Θ₂).
2. The angle of the first refraction (Θ₁) equals the second angle of incidence (Φ₂).

The minimum angle of deviation (α_o) is the least angle of deviation of the light ray in the prism at which the angle of incidence equals the angle of emergence.

When the minimum angle of deviation of the light in a triangular prism = 30°, this means that it is the least angle of deviation of the light ray in the prism at which the angle of incidence equals the angle of emergence = 30°.

Deduction of prism’s refractive index set at the minimum angle of deviation:

When the prism is in the position of minimum deviation:

Φ₁ = Θ₂ = Φ_o , Θ₁ = Φ₂ = Θ_o

α_o = 2 Φ_o − A   ∴  Φ_o = (α_o + A) / 2

A = 2 Θ_o             ∴   Θ_o = A / 2

n = sin Φ_o/sin Θ_o   ∴  n = sin ((α_o + A) / 2) / sin (A/2)

The apex angle of the prism is constant, Accordingly, as the refractive index of the prism differs for each color, the minimum angle of deviation also differs for each colour, When α_o increases, n increases also and vice versa, The refractive index (n) depends on the wavelength n ∝ 1 / λ   ∴  α_o depends on the wavelength.

Dispersion of the white light by a triangular prism: 

The white light consists of seven colours, each has its wavelength, Each colour has its angle of deviation, Accordingly, if a beam of white light falls on a prism set at the minimum angle of deviation, the emerging light disperses into seven spectral colours, red, orange, yellow, green, blue, indigo, and violet (arranged respectively from the apex of the prism to its base).

The violet colour has the maximum deviation, the maximum refractive index, and minimum wavelength, The red colour has the minimum deviation, the minimum refractive index, and maximum wavelength.

The thin prism

It is a triangular prism made of transparent material (glass) of an apex angle very small does not exceed 10° and is always set at the position of minimum deviation, There are some concepts related to the thin prism such as deviation angle, angular dispersion, and dispersive power.

Deviation angle

Deduction of deviation angle of the thin prism:

The thin prism is always in the position of minimum deviation, The refractive index of the prism’s material can be estimated from the relation:

n = sin ((α_o + A)/ 2) / sin (A / 2)

(α_o + A) / 2, A / 2 are small angles, then the sine of the angle equals the angle in radians.

∴ n = (α_o + A) / 2  ÷ (A / 2)

 n = (α_o + A)/A

∴  α_o + A = A n  , ∴  α_o = A ( n – 1 )

Factors that affect the angle of deviation in the thin prism :

1. The apex angle of the thin prism (A), is directly proportional.
2. The refractive index of its material (n), is directly proportional.

Where α_o in the thin prism does not depend on the first angle of incidence, The thin prism is always at the minimum angle of deviation.

Angular dispersion

Deduction of angular dispersion in thin prism:

The thin prism is always in the position of minimum deviation, It disperses the white light into the seven spectral colors, where:

The angle of deviation of the red light is estimated from the relation:

 (α_o)_r = A (n_r – 1)

The angle of deviation of the blue light is estimated from the relation:

 (α_o)_b = A (n_b – 1)

Where : (n_r) is the prism’s refractive index for red light and (n_b) is the prism’s refractive index for blue light.

 (α_o)_b − (α_o)_r = A (n_b – n_r)

The value [(α_o)_b − (α_o)_r] is called the angular dispersion between the blue and the red rays.

The angular dispersion between the blue and the red is the confined angle between the extensions of the emerged blue and red light rays after emergence from the prism or the difference between the deviation angles of the blue and the red colors.

When the angular dispersion between the blue colour and the red colour = 3°, this means that the confined angle between the emerged blue and red light rays = 3°.

 Factors affect the angular dispersion:

1. The apex angle of the prism.
2. The prism’s refractive index for both blue and red colors.

The yellow colour is considered the middle between the blue and red colour, The average refractive index (n_y) is the average refractive index between the blue and red colours, It is also the refractive index of yellow light (n_y),  n_y = (n_b + n_r) _/ 2.

The average deviation ( α_o )_y is the average deviation between the blue and red rays, It is also the deviation of yellow light (α_o)_y, (α_o)_y = ½ × [ (α_o)_b + (α_o)_r ].

Dispersive power

Deduction of dispersive power:

(α_o)_r = A (n_r − 1) ,  (α_o)_b = A (n_b − 1).

(α_o)_b − (α_o)_r = A (n_b − n_r)

The angle of deviation for the yellow light (middle between the blue and the red) is:

(α_o)_y = A (n_y − 1)

Where (n_y) is the refractive index for yellow.

If (α_o)_y is the average of (α_o)_b and (α_o)_r, then (n_y) is the average of (n_b) and (n_r). 

ω_α = ( ( α_o )_b − ( α_o )_r ) / ( α_o )_y

ω_α =  A ( n_b − n_r ) / A ( n_y − 1 )

ω_α =  ( n_b − n_r ) / ( n_y − 1 )

Where ω_α is the dispersive power and can be defined as :

The dispersive power of a prism (ω_α) is the ratio between the angular dispersion for the blue and red colours to the angle of deviation of the middle colour (the yellow).

When the dispersive power of a prism = 0.08, this means that the ratio between the angular dispersion for the blue and the red colours to the angle of deviation of the yellow colour = 0.08.

Factors affect the dispersive power of a thin prism :

The prism’s refractive index for the blue, red, and yellow colours.

Light wave properties, Analysis of white light, Spectrum colours and Light intensity

Types and Laws of light reflection, Regular & Irregular reflection of light

Light refraction effects, Law of light refraction, Mirage and Apparent positions of objects