Laws of circular motion (Centripetal Acceleration, Tangential linear Velocity & Centripetal Force)
Centripetal Acceleration
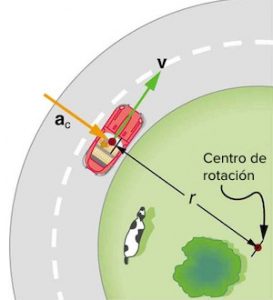
Changing the direction of velocity leads to the existence of acceleration called the centripetal acceleration ( a ) which is the acceleration acquired by an object moving in a circular path due to a continuous change in the direction of its velocity .
When a force ( F ) acts on a body of mass ( m ) moving at speed ( v ) in a circular path of radius ( r ) normally to the direction of its motion , The magnitude of velocity ( v ) remains constant along its path , The direction of velocity changes from one point to another on its path .
Finding the value of the centripetal acceleration
If a body moves from point ( A ) to point ( B ) , the velocity ( v ) changes in direction but maintains a constant magnitude .
a = v² / r
Factors affecting the centripetal acceleration ( a ) :
The tangential velocity : Centripetal acceleration is directly proportional to square of the tangential velocity at constant radius of the circular path .
Slope = a / v² = 1 / r
The radius of circular path : Centripetal acceleration is inversely proportional to the radius of the circular path at constant tangential velocity .
Slope = a r = v²
Tangential linear Velocity
Finding the tangential linear velocity : If the body complete one circular revolution in an interval of time ( T ) which is called the periodic time , Periodic time is the time taken by the body to make one complete revolution .
The tangential linear velocity = Distance ( circle circumference ) / Periodic time
v = 2 πr / T
Factors affecting the tangential linear velocity ( v ) :
The radius of circular path : Tangential velocity is directly proportional to the radius of the circular path at constant periodic time .
Slope = v / r = 2 π / T
The periodic time : Tangential velocity is inversely proportional to the periodic time at constant radius of circular path .
Slope = v T = 2 π r
v = 2 π r / T
Calculating the angular velocity :
If a body moves at tangential velocity ( v ) in a circle of radius ( r ) from point ( A ) to point ( B ) , covering a distance ( Δ l ) corresponding to an angle ( Δθ ) , during time interval ( Δ t ) .
Then the value ( Δθ / Δ t ) is known as the angular velocity ( ω ) .
ω = Δθ / Δ t
It is known that the value of the angle in radian equals the ratio between the arc length and the radius of the path .
Δθ = Δl / r
ω = ( Δl / Δ t ) × ( 1 / r ) = v / r ∴ v = ω r
Tangential ( linear ) velocity = Angular velocity × Radius of the path
Since v = 2 π r / T , then : ω r = 2 π r / T
∴ ω = 2 π / T
The Centripetal Force
Finding the Centripetal Force ( F ) , According to Newton’s Second Law , the force is given by the relation :
F = m a , a = v² / r
F = m a = m v² / r
Factors affecting the centripetal force ( F ) :
The object mass : Centripetal force is directly proportional to the object mass at constant tangential velocity and radius of circular path .
Slope = F / m = v² / r
The tangential velocity : Centripetal force is directly proportional to square of the tangential velocity at constant radius of circular path and object mass .
Slope = F / v² = m / r
F = m v² / r
The radius of circular path : Centripetal force is inversely proportional to the radius of the circular path at constant tangential velocity and object mass .
Slope = F r = m v²
Designing curved roads
It is necessary to calculate the centripetal force when designing the curved roads and railways in order to keep cars and trains moving along this curved path without skidding out .
If a car moves in a curved slippery road , the frictional forces may not be sufficient to turn the car around the curve , So , the car skids out the road .
Engineers define certain velocities for vehicles when moving in curves , If the vehicle velocity exceeds the predetermined velocity , the vehicle needs more more centripetal force to be kept in this curved path where F α v² .
It is forbidden for trucks and trailers to move on some dangerous curves , As the vehicle mass increases , it needs more centripetal force where F α m .
Slowing down in dangerous curves is a must to avoid accidents , As the radius of curve decreases the car needs more centripetal force to turn around , where F α 1/r .
When moving a bucket half filled with water in a vertical circular path at sufficient speed , the water does not spill out from the opening of the bucket because :
The centripetal force acting on water is normal to the direction of its motion , This force changes the direction of velocity without changing its magnitude to keep water inside the bucket rotating in a circular path .
We can make benefit of skidding objects out the circular path when the centripetal force is not sufficient to keep them rotating in the circular path :
- Making candy floss .
- Rotating barrels in amusement park .
- Drying cloths in automatic washing machines : water droplets adhere to clothes by certain forces , when the dryer rotates at great velocity , these adhesive forces will not be sufficient to hold these droplets , They separate from the cloths and move tangential to the circular path .
On using electric sharpener , the glowing metal splints blow in straight lines at tangent velocities .