Charles’s law, General gas law, Jolly’s law or pressure law, What is the Charles Law method?

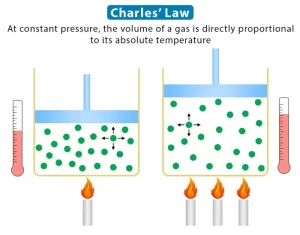
The gases contract by cooling and expand by heating, Equal volumes of different gases expand equally when heated through the same temperature rise, In other words, they have the same volume expansion coefficient, Charles’s law expresses the effect of temperature on the volume of a gas at constant pressure.

Charles’s law

All gases have the same volume expansion coefficient, at constant pressure, so the volume expansion coefficient (α_v) can be determined from the following relation:

α_v = Δ (V_ol) / [(V_ol)_0°C  Δt]

α_v = [(V_ol)_t − (V_ol)_0°C] / [ (V_ol)_0°C  Δt ]

The measuring unit of the volume expansion coefficient is (Kelvin)⁻¹ = (K⁻¹).

The volume expansion coefficient of gas at constant pressure (α_v) is the increase in volume at constant pressure per unit volume at 0°C for temperature rise, or it is the ratio between the increase in volume to the original volume at 0° C for 1° C rise in temperature at constant pressure.

When the volume expansion coefficient of a gas under a constant pressure = ( 1/273 ) K⁻¹, It means that the increase in volume at constant pressure per unit volume at 0° C for 1° C rise in temperature = 1/273 of the original volume.

To convert from Celsius to Kelvin, we use the following relation: T ( °K ) = t° C + 273

Where : (T) → Temperature on Kelvin scale, (t) → Temperature on Celsius scale.

Charles’s law: At constant pressure, the volume of a given mass of gas expands by 1/273 of its original volume at 0°C per each degree Kelvin rise in temperature, or at constant pressure, the volume of a fixed mass of gas is directly proportional to its temperature on Kelvin scale.

Charles’s law mathematical formula: V₁ / V₂ = T₁ / T₂

(V_ol)₁ / (V_ol)₂ = T₁ / T₂

T₁ = 273 + t₁,  T₂ = 273 + t₂

(V_ol)₁ / (V_ol)₂ = (273 + t₁) / (273 + t₂)

(V_ol)₁ / (V_ol)₂ = (1 + 1/273 t₁) / (1 +1/273 t₂)  , α_v = 1/273

∴ (V_ol)₁ / (V_ol)₂ = (1 + α_v t₁) / (1 + α_v t₂)

If two gases are mixed at constant pressure, then

(V_ol) / T (mix.) = [ (V_ol)₁ / T₁]  + [ (V_ol)₂ / T₂]

Jolly’s law or pressure law

Jolly’s law expresses the relation between gas pressure and its temperature at constant volume, The pressure of gases increases by increasing the temperature, and the increase in the pressure is constant for all gases.

At constant volume, the pressure of a given mass of a gas increases by increasing temperature, At constant volume equal pressures of different gases increase equally when heated to the same temperature.

The pressure expansion coefficient is constant for all gases, Equal pressures of different gases increase equally when heated through the same rise in temperature because the expansion coefficient for any gas at constant volume is constant.

At constant volume, the increase in the pressure (Δ P) is directly proportional to :

1. Original pressure at 0° C (P_o): Δ P ∝ P_{0° C}
2. Increase in temperature (Δ t): Δ P ∝ Δ t

∴  Δ P ∝ P_{0° C} Δ t

∴  Δ P = constant P_{0° C} Δ t

∴  Δ P = β_p P_{0° C} Δ t

Where (β_p) is the pressure expansion coefficient

β_p = Δ P / (P_{0° C} Δ t)

β_p = (P_t − P_{0° C}) / (P_{0° C} × Δ t)

The measuring unit of the pressure expansion coefficient is (Kelvin⁻¹) or K⁻¹.

The pressure expansion coefficient of a gas at constant volume (β_p) is the increase in pressure of a gas per unit pressure at 0° C when the temperature increases 1° C at constant volume.

Or it is the ratio between the increase in gas pressure to the original pressure at 0° C when the temperature rises 1° C at constant volume.

When the pressure expansion coefficient of a gas = 1/273 K⁻¹, It means that the increase in pressure of the gas per unit pressure at 0° C when the temperature increases 1° C at constant volume = 1/273 of the original volume.

The pressure expansion coefficient of a gas can be determined by knowing its pressure at t₁, t₂ at constant volume from the relation:

P₁ / P₂ = (1+ β_pt₁) / (1+ β_pt₂)

Jolly’s law or pressure law: The pressure of a given mass of gas, kept at constant volume, increases by 1/273 of its pressure at  0° C per each degree Kelvin rise in temperature, Or constant volume, the pressure of fixed mass of gas is directly proportional to its temperature on Kelvin scale.

The absolute zero (zero Kelvin) by using Charles’s apparatus: The absolute zero is the temperature at which the volume of an ideal gas vanishes theoretically at constant pressure.

When the absolute zero is = − 273° C, It means that the temperature at which the volume of the ideal gas vanishes theoretically at constant pressure = − 273° C.

The absolute zero (zero Kelvin) by using Jolly’s apparatus: The absolute zero is the temperature at which the pressure of an ideal gas vanishes theoretically at constant volume.

When the absolute zero is = − 273° C, It means that the temperature at which the pressure of the ideal gas vanishes theoretically at constant volume = − 273° C.

The temperature on the Kelvin scale is always positive value while the temperature on the Celsius scale may be positive or negative value.

General gas law

General gas law studies the gas behavior when changing the volume, pressure, and temperature of a gas together, Also explains the relation between the three variables together.

From Boyle’s law: V_ol ∝ 1/p, From Charles’s law:  V_ol ∝ T.

∴ V_ol ∝ T / P  ,  V_ol = constant T / P

P V_ol / T = constant

( P₁  (V_ol )₁) / T₁ = ( P₂  (V_ol )₂) / T₂

The general gas law: The product of the volume of a fixed mass of gas and its pressure divided by its temperature on the Kelvin scale equals a constant value.

ًWhen the gas at (STP), So, P = 1.013 × 10⁵ N/m², T = 273°K.

At the change of density of a gas at constant mass, So:

 P₁ / ρ₁ T₁ = P₂ / ρ₂ T₂

If two gases are mixed with each other, So:

( P V_ol / T ) ( mix. ) = ( P₁  ( V_ol )₁ ) / T₁ + ( P₂  ( V_ol )₂ ) / T₂

Gas laws, Boyle’s law, and properties of gaseous materials