Classification of Acids according to its strength (degree of ionization), Its source & Basicity

Acids can be classified according to its strength ( degree of ionization ) , Its source and Basicity , Acids are classified according to its degree of ionization in the aqueous solution into Strong acids and weak acids .

Classification of acids according to its strength ( degree of ionization )

Strong acids

The acids which are completely ionized in the water , Their aqueous solution conducts the electric current to a large degree, They are considered as strong electrolytes .

Examples : Hydroiodic acid HI, Hydrochloric acid HCl, Hydrobromic acid HBr, Sulphuric acid H₂SO₄, Nitric acid HNO₃ & Perchloric acid HClO₄ .

Weak acids

The acids which are incompletely ionized in the water , Their aqueous solution conducts the electric current to a small degree, They are considered as weak electrolytes .

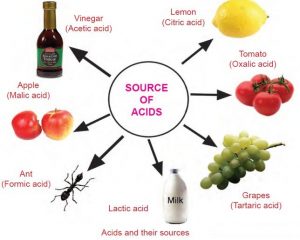
Examples : Carbonic acid H₂CO₃ , Phosphoric acid H₃PO₄ , Acetic acid ( vinegar ) CH₃COOH , Formic acid , Citric acid , Oxalic acid & Lactic acid .

There is no relation between the strength of the acid and the number of the hydrogen atoms in its molecular structure , Phosphoric acid ( H₃PO₄ ) is weaker than nitric acid ( HNO₃ ) , although it contains greater number of hydrogen atoms .

CH₃COOH ( aq ) + H₂ O ( l ) ↔ CH₃COO⁻ ( aq ) + H₃ O⁺ (aq)

Hydrochloric acid HCl is stronger than acetic acid because HCl is completely ionized in the water , but acetic acid is partially ionized in the water .

HCl ( aq ) + H₂ O ( l ) → Cl⁻ ( aq ) + H₃ O⁺ (aq)

Acids

Classification of acids according to their sources

Acids are classified according to their sources ( origin ) into Organic acids and Mineral acids

Organic acids

Acids that have an organic origin ( plant or animal ) , They are extracted from the organs of living organisms , All of them are weak acids .

Examples : Lactic acid ( milk products ) , Acetic acid ( vinegar ) , Citric acid ( from lemon ) , Oxalic acid and Formic acid .

Mineral acids

Acids that have no organic origin , They usually have non-metallic elements in their structure like chlorine , sulphur , nitrogen and phosphorus , Some of them are strong acids and others are weak .

Examples : Carbonic acid H₂CO₃ , Hydrochloric acid HCl , Phosphoric acid H₃PO₄ , Perchloric acid HClO₄ , Nitric acid HNO₃ & Sulphuric acid H₂SO₄ .

Classification of acids according to basicity

The basicity of acid 

It is the number of hydrogen ions ( H⁺ ) , which is produced by one molecule of the acid when it dissolves in the water .

Acids are classified according to the basicity into Monobasic acids ( Monoprotic ) , Dibasic acids ( Diprotic ) and Tribasic acids ( Triprotic ) .

Monobasic acids ( Monoprotic )

Acids where each molecule gives one proton H⁺ , when it dissolves in the water .

Examples : Organic monobasic acids ( Formic acid HCOOH , Acetic acid CH₃COOH ) , Mineral monobasic acids ( Hydrochloric acid HCl , Nitric acid HNO₃ ) .

Dibasic acids ( Diprotic )

Acids where each molecule gives one or two protons H⁺, when it dissolves in the water .

Examples : Organic diabasic acids ( Oxalic acid ) , Mineral dibasic acids ( Sulphuric acid H₂SO₄ , Carbonic acid H₂CO₃ ) .

Tribasic acids ( Triprotic )

Acids where each molecule gives one, two or three protons H⁺, when it dissolves in the water .

Examples : Organic tribasic acids ( Citric acid ) , Mineral tribasic acids ( Phosphoric acid H₃PO₄ ) .

Both of citric acid and phosphoric acid have the same degree of basicity, while they differ in their source ( origin), Because both of them are tribasic acids , but citric acid is an organic acid, while phosphoric acid is a mineral acid.

Classifications of bases according to strength ( degree of ionization ) and molecular structure

Properties of Acids and Bases & Theories defining acids and bases

Types of compounds, Properties of Acids, Bases (alkalis), Oxides and Salts