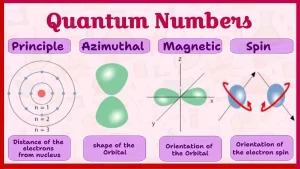
The quantum numbers and principles of distributing electrons

Quantum numbers

The mathematical solution of Schrodinger’s equation introduced four numbers that were called quantum numbers , to determine the energy of an electron in multi-electron atoms , we should know the four quantum numbers which describe it .

These four quantum numbers are :

1. The principal quantum number ( n ) : It describes the distance of the electron from the nucleus .
2. The subsidiary quantum number ( l ) : It describes the shapes of electron cloud in the sub-levels .
3. The magnetic quantum number ( m_l ) : It describes the shape and the number of the orbital in which the electron exists .
4. The spin quantum number ( m_s ) : It describes the spin of the electron .

The principal quantum number ( n )

Bohr had used this number in explaining the spectrum of hydrogen atom , it is given the symbol ( n ) and it is used to define the following :

The order of principal energy levels or electron shells , Their number in the heaviest known atom in its ground state is seven .

The number of electrons (e−) required to fill a given energy level which equals the formula 2n² ( two times the square of the shell number ) .

The principal quantum number has whose number values 1 , 2 , 3 , 4 , ……. etc , excluding zero , Each value is expressed by an alphabetical letter that represents a principal energy level , Energy levels increases from K to Q , K < L < M < N < O < P < Q .

The rule 2n² isn’t applied to the energy levels higher than the fourth level , because the atom becomes unstable , if the number of electrons exceeds 32 electrons in any level .

The subsidiary quantum number ( l )

It is given the symbol ( l ) , It determines the number of sub-levels in each principal energy level , Each principal energy level consists of a number of energy sub-levels equals to its principal quantum number .

The energy sub-levels take the symbols and values , Subsidiary quantum number ( l ) values [ 0 : ( n − 1 ) ] : Symbols of sub-levels , s = 0 , p = 1 , d = 2 , f = 3 )

There is a small difference in the energy of the sub-levels , They can be arranged according to increasing their energy , s < p < d < f .

Examples : What are the probable ( l ) values when n = 3 ?

Each principal energy level consists of a number of sub-levels which equals its numerical value , Number of sub-levels = 3 .

The probable ( l ) values range between [ 0 : ( n − 1 ) ] = [ 0 : ( 3 − 1 ) ] = 0 , 1 , 2

The magnetic quantum number ( ml )

It determines the number of orbitals within a certain energy sub-level from the relation ( 2l + 1 ) .

It determines the spatial orientation ( orientation in space ) of orbitals .

It is represented by the whole number values ( odd ) ranging between ( − l , ……. , 0 , …….. , + l ) .

The orbitals of the same sub-levels are equal in energy , but differ in direction and shape in space , Any orbital can’t be occupied by more than two electrons .

The p-sublevel is completely filled with 6 e⁻, while the d-sublevel is completely filled with 10 e⁻, Because the p-sublevel contains 3 orbitals, while the d-sublevel contains 5 orbitals and each orbital is filled with 2 e⁻.

Example : What are the probable ( m_l ) values when ( l = 2 ) ?

The probable ( m_l ) values ranges between −l , …… , 0 , …….., + l

The probable ( m_l ) values : −2 , −l , 0 , +1 , +2 

Example : Which of the following probabilities of the quantum numbers of a certain electron includes a mistake ?

1. n = 3 , l = 2 , m_l = − l
2. n = 4 , l = 3 , m_l = − 2
3. n = 1 , l = 1 , m_l = + l

The choice ( c ) , because when ( n = 1 ) the probable l and m_l values are ( 0 ) .

The spin quantum number ( m_s )

Since any orbital can not be occupied by more than two electrons , each electron spins on its own axis during its orbit around the nucleus as the spinning of the Earth on its own axis during its rotation around the Sun .

The spin quantum number determines the type of spin motion of the electron around its axis in the orbital , which is either :

• Clock wise ( ↑ ) with m_s value equals to ( + ½ ) .
• Anticlockwise (↓) with m_s value equals to ( − ½ ) .

The spin motion of the two electrons of the same orbital around their own axis arises a magnetic field in two opposite directions ( spin-paired state ) ( ↑↓ ) .

Orbitals have three different possibilities depending on the number of electrons located in them as follows :

• ( ) Empty orbital .
• ( ↑ ) Half-filled orbital contains one electron .
• ( ↑↓ ) full-filled orbital contains 2 pairing electrons that have opposite spins and called spin paired state .

Although the two electrons of the same orbital carry the same negative charge , they do not repel with each other , because the magnetic field arises from the spinning of one electron is in a direction opposing the direction of the other magnetic field arising from spinning of the other electron and that decreases the repulsive force between the two electrons .

Summary of the relationship between the principal energy level , sub-levels and orbitals .

Each principal energy level :

• Consists of a number of sublevels equals its number ( n = no. of l values ) .
• Consists of a number of orbitals equals the number of the level ( n² ) .
• The number of electrons occupying it , equals two times the square of the level number ( 2n² ) .

Each sublevel consists of a number of orbitals which equals ( 2l + 1 ) .

Each orbital occupied by 2 electrons : ( s = 2 , p= 6 , d = 10 , f = 14 ) .

Principles of distributing electrons

There are some important rules , which must be considered in distributing electrons in the atom , These rules are :

1. Pauli’s exclusion principle .
2. Aufbau ( building-up ) principle .
3. Hund’s rule .

Pauli’s exclusion principle

Pauli’s exclusion principle : It is impossible for two electrons in the same atom to have the same four quantum numbers .

When ( np ) sublevel contains one electron , it is not necessary to be :

( m_l = − l ) , but it may be equal 0 or + l

( m_s = + ½ ) , but it may be equal − ½

Aufbau ( building-up ) principle

Aufbau ( building-up ) principle : Electrons occupy the sub-levels in the order of increasing their energy , the lowest energy sub-levels are filled firstly .

The sub-levels of the same principal energy level differ slightly from each other in energy .

Arrangement of sub-levels according to their energy depends on :

Sum of ( n + l ) , Ex : Energy of 4s sub-level is lower than that of 3d sub-level , because sum of ( n + l  ) of 4s sub-level is less that of 3d sub-level .

Order of the principal energy level , in case of equality of sum ( n + l ) values for two sub-levels , Ex : Energy of 3_p sub-level is lower than that of 4s sub-level , Because ( n ) value of 3_p sub-level is lower than that of 4s sub-level .

The sequence of energy sub-levels is arranged ascendingly according to their energy follows 

The order : 1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5d < 6s < 4f < 5d < 6p < 7s < 5f < 6d < 7p

Filling the energy sublevels : s up to 2 electrons , p up to 6 electrons , d up to 10 electrons , f up to 14 electrons .

The electron configuration for one of the energy levels can be expressed as the following : 2p⁶

Where , 2 is the principal energy level ( n ) , p is the energy sub-level , 6 is number of electrons in the orbitals of sub-level .

Example : write the electron configuration for the following elements , according to building-up principle : ₁₁Na , ₂₀Ca , ₃₀Zn , ₁₉K , ₂₆Fe .

₁₁Na : 1s² , 2s² , 2p⁶ , 3s¹

₂₀Ca : 1s² , 2s² , 2p⁶ , 3s² , 3p⁶ , 4s²

₃₀Zn : 1s² , 2s² , 2p⁶ , 3s² , 3p⁶ , 4s² , 3d¹⁰

₁₉K : 1s² , 2s² , 2p⁶ , 3s² , 3p⁶ , 4s¹

₂₆Fe : 1s² , 2s² , 2p⁶ , 3s² , 3p⁶ , 4s² , 3d⁶

Hund’s rule

Hund’s rule : No electron pairing takes place in a gives sub-level until each orbital contains one electron .

Rules of filling the energy sub-levels with electrons , according to Hund’s rule :

1. The orbitals of the same sub-levels are equal in their energy .
2. The orbitals of the same sub-levels are filled by the unpaired electrons firstly , The spin of single electron in the same direction gives the atom stability .
3. When the two electrons are paired in one orbital , they have opposite spins , to decrease the repulsive force between them , then the two electrons are in a spin-paired .
4. Electrons pairing takes place in the orbitals of the same sub-level after occupying all orbitals by unpaired electrons .
5. The electrons prefers to be paired with another electron in one orbital of the same sub-level rather than being transferred to a higher energy sub-level . 

The spin of single electrons in the same sub-levels orbitals is in the same direction , because this state gives the atom more stability .

The electron prefers to occupy an orbital alone in the same sub-level rather than pairing with another one in the same orbital , Because when two electrons are paired in one orbital , ( in spite of their opposite spins ) , there must be a repulsive force that decreases the stability of the atom ( increasing in its energy ) .

The electron prefers pairing with another one in orbital in the same sub-level rather than transferring to the higher energy sub-level , because the required energy to overcome the repulsive force between the two paired electrons is less than that is required for transferring the electron to a higher sub-level .  

Example : Predict the atomic number for each of the following elements :

An element whose electronic configuration is 1s² , 2s² , 2p³ → 7

An element whose principal energy level ( n = 3 ) contains 3 electrons → The electronic configuration : 1s² , 2s² , 2p⁶ , 3s² , 3p¹ , So , the atomic number = 13

An element whose last 3s-sublevel is half-filled with electrons → The electronic configuration : 1s² , 2s² , 2p⁶ , 3s¹ , So , the atomic number = 11 .

Atoms components , Rutherford and Bohr’s Atomic Models

Atomic emission spectra , Bohr’s atomic theory & Wave mechanical theory of the atom

Modern periodic table and classification of Elements
‏
‏