Physical quantities, Scalar Quantities, Vector quantities and Finding resultant of two perpendicular forces

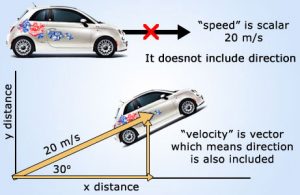
Physical quantities can be classified into Scalar and Vector Quantities, A Scalar quantity is a physical quantity that can be fully defined by its magnitude only and it has no direction while a Vector quantity is a physical quantity that can be fully defined by both magnitude and direction.

Scalar and Vector Quantities

Examples of Scalar quantity are distance, Mass, Time, Temperature, and Energy, Examples of Vector quantity: Displacement, Velocity, Acceleration, and Force.

When measuring a physical quantity such as Temperature (The magnitude of temperature say, 27 ° C describes temperature fully), Velocity (A value of 20 km/h does not describe fully the velocity of a car such that the direction of the car motion should be defined).

Distance and Displacement

There is a difference between the concept of displacement and the concept of distance, Distance is the length of the path moved by an object from one position to another, and Distance is a scalar quantity that can be fully defined by its magnitude only.

Displacement is the length of the straight line segment in a given direction between the starting point and the endpoint, Displacement is a vector quantity that can be fully defined by its magnitude and direction.

Guidelines to solve problems

• If an object moves in one direction from A to B, the magnitude of displacement equals the distance covered.
• If an object moves in one direction from A to B and then returns back to A, the magnitude of displacement = 0 and the distance covered = 2 AB.
• If an object moves in a curved path from A to B, Displacement would be shorter than distance.
• If an object moves in one direction from A to B and then reverses its direction to C, then the displacement ( d ) = AB – BC, and The distance ( s ) = AB + BC.

Representation of vector quantities 

The vector quantity is represented by a directed straight segment (→) whose base is at the starting point and its tip is at the endpoint, where its length is proportional to the vector magnitude, The arrow direction points to the direction of the vector quantity, The vector quantity is denoted by a bold letter (A) or a letter tagged by a small arrow.

Some basics and vector algebra 

Two vectors are equal when they have the same magnitude and the same direction (even if they have different starting points), Two vectors are not equal when they have different directions (even if they have the same magnitude) or different magnitudes (even if they have the same direction).

Vector Algebra

Vector Algebra such as Vectors addition, Vector resolution, Vector product (Scalar (dot) product and Cross product).

Resultant (addition) of vectors

When two forces or more act on an object, this object moves in a certain direction determined by the resultant of these forces, The resultant force is a single force that produces the same effect on an object as that produced by the original acting forces.

Application

If a rock is pulled by two ropes with two forces of 30 N and 40 N having an angle of 90° between them, We notice that the rock is moved a certain distance in a direction different than those of the two forces (during a certain time).

If the two ropes are replaced by one rope and pulled by a force of 50 N, We notice that the rock is moved through the same distance in the same direction when it is affected by the two forces at the same time.

This means that the force 50 N produces the same effect as that of the two forces 30 N and 40 N, So, it is considered the resultant of the two forces 30 N and 40 N.

There are two ways to add two vectors by drawing a triangle and by drawing a parallelogram in which A and B are adjacent sides, Thus, the diagonal represents their resultant.

Finding the resultant of two perpendicular forces

First: Graphically

1. Draw a horizontal line (AB), on the graph paper, of length 3 cm to represent the first force (F1 = 3 N).
2. Perpendicular to (A B) at the point (A), draw a vertical line (AD) of length 4 cm to represent the second force (F2 = 4 N).
3. Complete the rectangle ABCD.
4. Join the diagonal (AC) to represent the magnitude and direction of the resultant.
5. Measure the length of the line segment (AC) that represents the magnitude of the resultant force.
6. Measure the angle (BAC) that defines the direction of the resultant force relative to the first force (F1).

Second: Theoretically

Find the magnitude of the resultant force using Pythagoras’ theorem for the right-angled triangle (AC² = AB² + BC²).

F² = F₁² + F₂² 

We can find the angle (θ) by the relation

tan θ = F_y / F_x = F₂ / F₁

Resolution of a vector

Resolution of a vector is the reverse operation for getting the resultant of some vectors where a force can be resolved into two perpendicular forces along dimensions (x, y), Thus:

F_y = F sin θ

F_x = F cos θ

Product of vectors

There are different forms of finding the product of two vectors:

Scalar (dot) product

The dot product of two vectors A and B is expressed as follows:

A . B = A B cos θ

The sign (.) is pronounced ” dot “, The result is a scalar quantity.

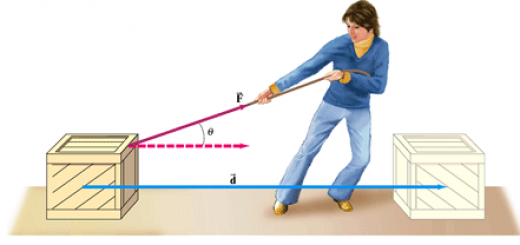
The work is a scalar quantity as it is the dot product of two vectors which are force and displacement, W = F. d If the vector (F) acts on the vector (d) at an angle (θ).

W = F D cos θ

Vector (cross) product

The cross product of two vectors A and B is expressed as follows:

C = A ^ B = A B sin θ n

Where n is a unit vector perpendicular to the plane of both vectors A and B, The sign (^) is pronounced cross and the result is a vector quantity C, The vector C points to the direction of n perpendicular to the plane of both vectors A and B.

The operation of the electric motor depends on the presence of two vectors which are the electric field and magnetic field, while they cause the rotation of the motor coil in a direction perpendicular to the plane of both.

The right-hand rule

It is used to define the direction of the vector product C of two vectors A and B.

How to apply?

Move the fingers of the right hand from the first vector towards the second vector through the smaller angle between them θ, the thumb then points to the direction of their vector product.

You can follow science online on YouTube from this link: Science online

You can download Science Online application on Google Play from this link: Science online Apps on Google Play

Static objects, Moving objects, Types of Motion and Velocity