Neurosecretion types, Function of Dopamine, Serotonin, Melatonin and Histamine
Neurosecretions are classified into two groups: Neurotransmitters are released into the synaptic cleft in order to influence neighboring cells. They have a short range and a short life span. Neurohormones are released into the blood, allowing them to cover larger distances. However, some neurotransmitters simultaneously function as neurohormones.
Synaptic signal transmission
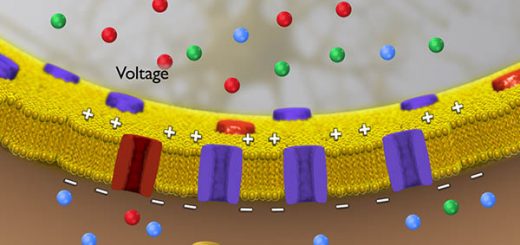
The chemical synapses function according to a similar principle, In the area of the synapse, the surface of the signaling cell (presynaptic membrane) is separated from the surface of the receiving cell (postsynaptic membrane) only by a narrow synaptic cleft.
When an action potential reaches the presynaptic membrane, voltage-gated Ca2+ channels integrated into the membrane, open and trigger exocytosis of the neurotransmitter stored in the presynaptic cell, Neurotransmitters are substances that are produced by the neurons, stored in the synapses, and released into the synaptic cleft in response to a stimulus:
- At the postsynaptic membrane, they bind to special receptors and affect their activity.
- Each neuron usually releases only one type of neurotransmitter, Neurons that release dopamine are referred to as “dopaminergic” while those that release acetylcholine are cholinergic” etc.
- The transmitters that are released diffuse through the synaptic cleft and bind on the other side to receptors on the postsynaptic membrane. These receptors are integral membrane proteins that have binding sites for neurotransmitters on their exterior.
Neurotransmitter receptors are divided into two large groups according to the effect produced by binding of the transmitter:
A. Ionotropic receptors are ligand-gated ion channels. When they open as a result of the transmitter’s influence, ions flow in due to the membrane potential. If the inflowing ions are cations (Na+, K+, Ca2+), depolarization of the membrane occurs and an action potential is triggered on the surface of the postsynaptic cell. This is the way in which stimulatory transmitters work (e. g. acetylcholine and glutamate).
By contrast, if anions flow in (mainly CI–), the result is hyperpolarization of the postsynaptic membrane, which makes the production of a postsynaptic action potential more difficult. The action of inhibitory transmitters such as glycine and y-aminobutyric acid (GABA) is based on this effect.
B. Metabotropic receptors: after binding the transmitter, these interact on the inside of the postsynaptic membrane with G-proteins, which in turn activate or inhibit the synthesis of second messengers. Finally, second messengers activate or inhibit protein kinases, which phosphorylate cellular proteins and thereby alter the behavior of the postsynaptic cells.
Classification of neurotransmitters
The neurotransmitters are classified into many groups according to their chemical structure.
Acetylcholine
Acetylcholine (ACh) is a simple molecule synthesized from choline and acetyl-CoA through the action of choline acetyltransferase, Neurons that synthesize and release ACh are termed cholinergic neurons, It functions in both the CNS and the PNS.
The cholinergic receptors are 2 receptor classes: muscarinic (metabotropic) and nicotinic (ionotropic); within the PNS, ACh is the major transmitter acting at neuromuscular junctions, where it triggers muscle contraction, and in certain parts of the brain its major effects are inhibitory.
When the action potential reaches the terminal button of the presynaptic neuron a voltage-gated calcium channel is opened, The influx of calcium ions, (Ca2+), stimulates the exocytosis of presynaptic vesicles containing ACh, which is thereby released into the synaptic cleft, Once released, ACh must be removed rapidly in order to allow the repolarization to take place; this step of hydrolysis is carried out by the enzyme, acetylcholinesterase.
Myasthenia Gravis (MG) is an auto-immune disease associated with antibodies to the ACh receptors of the neuromuscular junction, The binding of the antibodies to the receptor results in receptor destruction, In the severe form of MG, the muscles of the diaphragm become affected resulting in respiratory failure which contributes to the mortality of MG, Treatment of M involves the use of acetylcholinesterase inhibitors, The use of these types of drugs allows for enhanced levels of Ach at the motor endplate during repeated muscle stimulation.
Catecholamines
The principal catecholamines are norepinephrine, epinephrine, and dopamine, These compounds are formed from tyrosine. Tyrosine is produced in the liver from phenylalanine through the action of phenylalanine hydroxylase, The tyrosine is then transported to the catecholamine-secreting neurons where a series of reactions convert it to dopamine, norepinephrine, and finally to epinephrine.
The catecholamine neurotransmitter and hormone; binds to both α- and β-adrenergic receptors (GPCRs); produced in the adrenal medulla and neurons in the CNS and PNS; primary hormone of the fight-or-flight response of the sympathetic nervous system; is a major regulator of the metabolic processes in numerous tissues; regulates heart rate, induces vasoconstriction and bronchodilation.
The catecholamine neurotransmitter produced in CNS is the major neurotransmitter function is in the regulation of cardiac inotropic (force) and chronotropic (rate) activities.
Catecholamine catabolism
- A small percentage of epinephrine is excreted in the urine. Catecholamines cannot penetrate the blood-brain barrier. Thus, the norepinephrine in the brain must be synthesized with the brain tissue.
- Most of the hormones are metabolized in the tissues by a series of methylations of the phenolic group and oxidations of the amide side chains.
- Catechol O-methyl transferase (COMT) catalyzes the addition of methyl group, on the benzene ring using S-adenosyl methionine as a methyl donor.
- Monoaminoxidase (MAO) deaminates monoamine, It occurs mainly in the liver, stomach, kidney, and intestine.
- One of the principal metabolites of epinephrine and norepinephrine is vanillyl mandelic acid (VML which increases in the urine of patients with pheochromocytoma tumors of the adrenal medulla).
Dopamine
In the CNS dopamine plays a major role in feeding; also involved in motor control; in the periphery, dopamine regulates the release of several hormones such as insulin from the pancreas & norepinephrine from blood vessels; functions by binding to a family of dopaminergic receptors (GPCRs).
The neurological disorder Parkinson’s disease is associated with underproduction of dopamine, and it has traditionally been treated by administering L-dopa, Overproduction of dopamine in the brain may be linked to psychological disorders such as schizophrenia.
Serotonin
Serotonin (5-hydroxytryptamine, 5HT) is formed by hydroxylation of tryptophan by tryptophan hydroxylase in the liver. This is a mixed function of oxygenase that forms 5-hydroxytryptophan. The latter is then decarboxylated to serotonin (5-hydroxy tryptamine) by a pyridoxal phosphate-dependent enzyme.
Serotonin is found in the intestine most abundantly expressed in enterochromaffin cells of the gut where it regulates motility and acts as a transmitter to release peptide hormones; Also 5-HT is found in platelets; released from activated platelets where it stimulates further activation propagating role of platelet aggregation in coagulation.
In the CNS 5-HT regulates mood, appetite, sleep, memory, and learning; selective serotonin reuptake inhibitors (SSRIs) used in the treatment of depression.
Catabolism of serotonin
- Oxidative deamination of serotonin by monoamine oxidase will form 5-hydroxyindole acetic acid (5-HIAA) (normal value 2-8 mg/24-hour urine),
- In depression also, we can give a drug that inhibits monoamine oxidase enzyme to prevent the decrease in serotonin level.
Melatonin
It is a hormone, derived from tryptophan serotonin is an intermediate. Melatonin is formed in the pineal body tissue and in the peripheral nerves of man and secreted into the blood and CSF. Melatonin is synthesized in humans during the dark period of the day and maintained at a low level during the daylight.
Histamine
It is synthesized by decarboxylation of histidine. It is produced by mast cells and basophils; Histamine is released from mast cells when allergens bind to IgE-antibody complexes: there are four histamine receptors (H1-H4), Enterochromaffin-like cells of the stomach also secrete histamine which stimulates gastric parietal cells to secrete acid, It is also present in the hypothalamus.
γ-aminobutyrate (GABA)
Many amino acids have distinct excitatory or inhibitory effects upon the nervous system. The amino acid derivative, y-aminobutyrate (GABA) is a well-known inhibitor of presynaptic transmission in the CNS. and also in the retina, It exerts effects in the periphery: binds to two classes of receptors termed GABA-A (ionotropic) and GABA-B (metabotropic).
GABA formation occurs by the decarboxylation of glutamate catalyzed by glutamate decarboxylase (GAD), GAD is present in many nerve endings of the brain as well as in the β-cells of the pancreas, The activity of GAD requires pyridoxal phosphate (PLP) as a cofactor The underproduction of GABA occurs due to GAD or vitamin B6 deficiency; it is associated with epileptic seizures.
Glutamate
It is the most abundant excitatory neurotransmitter in the CNS: glutamate binds to the metabotropic glutamate receptors (mGluRs). Glutamate also binds to several ionotropic receptors like the N-methyl-D-aspartate receptor (NMDAR).
Glycine
It is an inhibitory neurotransmitter in the CNS primarily within the brainstem, spinal cord, and retina binds to glycine receptors (GlyR) ionotropic.
Peptides
Peptides make up the largest group among the neurosecretions, Many peptide hormones e.g. angiotensin Il simultaneously act as transmitters, Most neuropeptides are small, Endorphins and enkephalins are a particularly interesting group of neuropeptides, They act as ”endogenous opiates” by producing analgesic, sedative, and euphoriant effects in extreme situations, Drugs such as morphine and heroin activate the receptors for these peptides.
Purine derivatives
Purine derivatives with neurotransmitter function are all derived from adenine-containing nucleotides or nucleosides. ATP is released from sympathetic, sensory, and enteric nerves; ATP binds to the metabotropic G-protein coupled receptors (GPCR) of the P2Y family of purinergic/pyrimidinergic primarily expressed on the surface of platelets where it serves as a major ATP-mediating receptor of the blood coagulation.
ATP also binds to the ionotropic family of purinergic receptors (P2X); these receptors modulate synaptic transmission throughout the autonomic nervous systems of the CNS, Adenosine is an inhibitory neurotransmitter within the CNS, and suppresses arousal thus promoting sleep.
The stimulatory effect of caffeine is mainly based on the fact that it binds to adenosine receptors (members of GPCR family). In the periphery adenosine exerts anti-inflammatory actions, stimulates vasodilatation through vascular smooth muscle, and induces bronchospasm in the lungs.
You can subscribe to Science Online on YouTube from this link: Science Online
You can download the Science Online application on Google Play from this link: Science Online Apps on Google Play
Metabolism of the brain, Cerebrospinal fluid function, location and symptoms
Ventricular system of the brain, Boundaries of 4 ventricles & pathway of Cerebrospinal (CSF)
Cerebellar cortex structure, function, location, layers & fibers
Cerebellum function, structure, anatomy, location & blood supply
White matter of the brain function, structure and Blood supply of the internal capsule
Function and Physiology of Thalamus, Hypothalamus & Limbic system